Part 1 aFC Vision: 1.0. Creation of the 'Football World' in the Unbounded Landscape
Proto Perception and Cognition of the Unbound Playing Ground Landscape
- Part 1 aFC Vision
- 0. Creation of the 'Football World' in the Unbounded Landscape
- 0.1. Gon's Cognition of the Unbounded Landscape
- 0.2. Gon’s Local and Global Symmetry Exploration of the Unbounded Landscape
- 0.3. Gon’s Exploitation of the Constrained Unbounded Landscape
- 0.4. Gon Must Gain Ball Location Space and Take Control of the Ball
- 0.5. The Bounded Landscape
Part 1 aFC Vision
0. Creation of the 'Football World' in the Unbounded Landscape
Charles R Paez Monzon 2020 aNatureTechnologies
Gon, "must perceive in order to move, but he must also move in order to perceive" [Gibson]
Gos is the Football World's creator
0.1. Gon's Cognition of the Unbounded Landscape
0.1.1. The Universe of Football's Big-Bang
#collapse_hide
# Base Computational Geometry of the Environment in Python
#Set of Fundamental packages
from __future__ import print_function
import numpy as np
import scipy
import scipy.spatial
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
import ipywidgets as widgets
import moviepy as mpy
#import triangle
#import circumcircle
from datetime import datetime
from matplotlib.patches import Polygon, Arc, Ellipse
from ipywidgets import interact, interactive, fixed, interact_manual
from IPython.core.interactiveshell import InteractiveShell
from IPython.display import display
from IPython.display import display_html, display_jpeg, display_png, display_json, display_latex, display_pretty, display_svg
from IPython.display import Image
from moviepy.editor import VideoClip
from moviepy.video.io.bindings import mplfig_to_npimage
#from matplotlib import colors
#%matplotlib inline
#%matplotlib ipympl
#%matplotlib widget
%load_ext autoreload
%autoreload 2
%config InlineBackend.figure_format = 'retina'
plt.style.use('fivethirtyeight')
For Gon the Universe of Football's Big-Bang happens when he sees a ball in the open, for first time. For us, when he enters in our empty natural pitch for first time and his AcEmFC trainer invites him to experience it as an 'unbounded landscape'.
Gon experiences the proto-state of a non-phenomenical unbounded landscape with no space-time, where there is neither things (no ball, no goals, no stadium, etc) nor human beings (no players, no head coaches, no arbiters, no spectators, etc), and therefore only his unary actions are possible; that constitute unary-events.
- The set of things is empty: {}
- The set of agents is empty: {}
- The set of events is empty: {}
Gon is standing now in an arbitrary point in open space and this is the proto-state in a proto-spice of a space-no-time unbounded landscape shown in Figure 1.0.1.
- The set of things is empty: {}
- The set of agents is a singleton: {Gon}
- The set of events is empty: {}.
#collapse_hide
IcHx = 105.0
IcHy = 105.0 # In AcEmFC is 68.0
GOAL = 7.32/IcHy*100
ls_col = 'darkseagreen' # landscape color
llm_col = 'white' # landscape line marks color
sid_col = 'gold' # space id color
edge = 'blue'
bgcolor = 'yellow'
lw = 1.0
zorder = 1
alpha = 1
# Gon's coordinates
xs = 50.0
ys = 50.0
#collapse_hide
def draw_landscape():
"""
Sets up unbounded landscape
Returns matplotlib fig and axes objects.
"""
fig = plt.figure(figsize=(IcHx/15, IcHy/15))
fig.patch.set_facecolor(ls_col) # outside the football frame
axes = fig.add_subplot(1, 1, 1)
axes.set_facecolor(ls_col) # inside the football frame
axes.xaxis.set_visible(False)
axes.yaxis.set_visible(False)
axes.set_xlim(0,100)
axes.set_ylim(0,100)
axes.set_axis_off() # do not draw spindles
axes = draw_patches(axes)
axes = draw_Gon(xs,ys)
return fig, axes
def draw_patches(axes):
plt.xlim([-5,105])
plt.ylim([-5,105])
#pitch
axes.add_patch(plt.Rectangle((0, 0), 100, 100,edgecolor=ls_col, facecolor="none", alpha=alpha))
#half-way line
#axes.add_line(plt.Line2D([50, 50], [100, 0],
# c=llm_col))
#goals
axes.add_patch(plt.Rectangle((100, (100-GOAL)/2), 1,GOAL,ec=llm_col, fc='none'))
axes.add_patch(plt.Rectangle((0, (100-GOAL)/2),-1,GOAL,ec=llm_col, fc='none'))
#halfway concentric circles
#halfway concentric circles
axes.add_patch(Ellipse((50, 50), 0.5*55/IcHx*100, 0.5*55/IcHy*100,
ec=llm_col, fc='none',zorder=1))
axes.add_patch(Ellipse((50, 50), 1*55/IcHx*100, 1*55/IcHy*100,
ec=llm_col, fc='none',zorder=1))
axes.add_patch(Ellipse((50, 50), 2*55/IcHx*100, 2*55/IcHy*100,
ec=llm_col, fc='none',zorder=1))
#axes.add_patch(Ellipse((50, 50),2*55/IcHx*100, 2*55/IcHy*100,ec=llm_col,fc='none',lw=1.0))
# cognitive knowledge acquired
plt.text(40,43,'the near by',fontsize=16, color=sid_col) #-5,110
plt.text(40, 7,'the far away',fontsize=16, color=sid_col) #-5,110
plt.text(40,66,'inner',fontsize=16, color=sid_col) #-5,110
plt.text(40,90,'outter',fontsize=16, color=sid_col) #-5,110
#plt.savefig('../../APimages/03ULandscape.png')
return axes
def draw_Gon(x,y):
plt.scatter(x,y,edgecolor=edge,linewidth=lw,facecolor=bgcolor,alpha=0.8,zorder=4,s=100)
return
#collapse_hide
draw_landscape()
0.1.3. Explore and Exploit the Environment Constrained by His Vision Field
Gon has nil information about the environment. So, he can not exploit its knowledge about it (neither the landscape nor the game with the ball). He has first to explore around the unbounded landscape from the basic unary-action of being in stasis standing.
Gon has in vision his most commonly used dimension of perception of his uncertain enviroment. His vision field is a sensory source of information in which base his decision making and intentional actions to execute in the unbounded landscape. Where to move is the first agency problem he must solve.
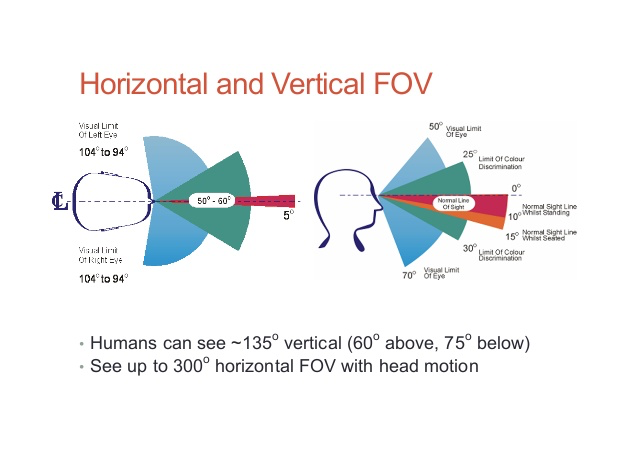
Gon has a limited field of vision, like any human, from about 180-200 degrees horizontally determined by the combination of foveal (looking standing) and peripheral (looking moving head on his shoulders) visions. Therefore in any standing position at any time, there is a blind zone between 160-180 degrees that Gon is unable to see. By moving his head can see up 300 degrees horizontally, as shown in Figure 1.0.2.
The visual perception of movement is a very important factor in the mantainance of equilibrium, where peripheral vision plays an important role.
Collecting visual information, when Gon is in stasis, in the unbounded landscape means "a picture taken of reality by our (Gon's) mind" [Bergson]:
- scanning the landscape by moving his head and checking on his shoulders Gon is able to collect information from surroundings.
- correcting his body orientation to see relevant affordances offered by the unbounded landscape
These skills reduce Gon’s blind zone constrains significantively. Gon understands the meaning of affordances offered for the environment as “opportunities to move”. He is observing the open space process and gets the impression of stasis all around the unbounded landscape.
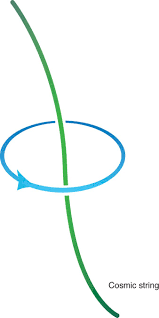
Gon will find out, in the proto space-time, in which direction he must take to move his body. He will perceive the infinite set of affordances or opportunities of actions in the omnidirectional open space that emerges and that are offered to him.
- In any direction chosen to explore, he looks the same scene:
- an unbounded 2D plane surface of open space.
-
All local information gathered in any point in the environment is uniform and the same.
- This means that there is a symmetry in the first-state that Gon has to explore. This is the reason to call this experience the cosmic string [Witten] in the unbounded, uniform landscape that exhibits an invariant 2π rotational symmetry: “The infinite affordance”.
Therefore, in principle,
-
there is no need of global exploration of the unbounded field because any local information about is the same in any other place and therefore, the local information is in coherence, in entanglement with the global information; because the environment is a space-no-time fabric.
-
Gon has local and global freedom to choose a second unary-action of move anywhere to any location near by or far away in an open spatial-time unbounded landscape fabric.
Gon has founded, as an organism in an environment, an organismic Universe [Bergson, Teillard, Mae-Wan Ho] and he is able to understand that he is the creator of an evolving process with his agency dynamics and, that a space-time inseparable, mutable process can be experienced and understands from inside in the open. A Gon-unbounded landscape system that is in coherence as a whole. There is an embodiness creative and participatory entanglement between Gon and a 'certain' landscape.
The AcEmFC’s trainer throws a ball to an arbitrary location in the field and Gon, who is in stasis-standing, understands it is for him; for playing the ball with his feet. Now on, with the global constrain: Football is just a 'game' for move around to open space, move to the ball, and play with the ball in a game that pursues to score goals in 1-out-of-2-goals.
0.3.1. Goals and ball in stasis in a constrained unbounded landscape
-
The AcEmFC’s trainer created a perturbation of the first-state and evolved the system to a constrained second-state that emerges globally when goals and a ball are contained in the unbounded landscape in positional stasis. In this state, a proto space-no-time is created where there is a conservation of momentum of the ball in stasis or no movement of the ball in such any place.
- The set of things is: {goals, ball}
- The set of agents isa singleton: {Gon}
- The set of events is a singleton: {stasis,} = {positional_stasis,}
A 'here-now', where the 'illusion of time' emerges. Gon understands that he must disturb the relativistic state of football in stasis in an arbitrary point all around the constrained unbounded landscape over an horizon of ordered events.
0.3.2. Gon has to explore and identify the location of the ball with his vision field through the unbounded landscape while he is in out-of-ball-control state
Gon is standing in an arbitrary point p, let us assume that the ball is located in Gon’s blind zone of vision. Gon is in stasis in a universe characterized by a second state of space-no-time. The system evolves to a third relational state where an agent with a proto-knowledge must exploit his knowledge about a constrained unbounded landscape.
- The set of things is a triple: {goals,ball}
- The set of agents is a singleton: {firstman} = {Gon}
- The set of events is a tuple: {positional_stasis,standing_exploring, move_to_open_space, move-to_the_ball}.
In this third-state,
- Gon knows that he, himself is a generator of intentional own body’s transformations in the enviroment.
- Gon new exploration of the constrained unbounded landscape breaks the rotational symmetry.
- Now on, he experiences the difference of the complete local freedom and the constrained global information.
This experience is materialized in the sense of sidewayness or laterality and counter-sidewayness or counter-laterality subspaces. Football game is about to create xG opportunities at the end-up part where an effective contralateral action will put the ball on the net of the others goal on and to block it to happen in our goal.
#collapse_hide
uls_col = 'darkseagreen' # unbounded landscape color
vfl_col = 'gold' # visual field limits color
ball_edge = 'black'
ball_col = 'black'
# ball coordinates
xb = 60.0
yb = 77.0
#collapse_hide
def draw_landscape_s3(ball_ref, dbs):
"""Sets up unbounded landscape
Returns matplotlib fig and axes objects.
"""
fig = plt.figure(figsize=(IcHx/15, IcHy/15))
fig.patch.set_facecolor(uls_col) # outside the football frame
axes = fig.add_subplot(1, 1, 1)
axes.set_facecolor(ls_col) # inside the football frame
axes.xaxis.set_visible(False)
axes.yaxis.set_visible(False)
axes.set_xlim(0,100)
axes.set_ylim(0,100)
axes.set_axis_off() # do not draw spindles
draw_Gon(xs,ys)
draw_Ball(xb,yb)
axes = draw_patches_s3(axes,ball_ref,dbs)
return fig, axes
def draw_Ball(x,y):
plt.scatter(x,y,edgecolor=ball_edge,linewidth=lw,facecolor=ball_col,alpha=1.0,zorder=4,s=20)
return
def draw_patches_s3(axes,ball_ref,dbs):
plt.xlim([-5,105])
plt.ylim([-5,105])
#pitch
axes.add_patch(plt.Rectangle((0, 0), 100, 100,
edgecolor=ls_col, facecolor=ls_col, alpha=1))
#goals fc='none'
axes.add_patch(plt.Rectangle((100, (100-GOAL)/2), 1, GOAL,
ec='w', fc=ls_col))
axes.add_patch(plt.Rectangle((0, (100-GOAL)/2), -1, GOAL,
ec='w', fc=ls_col))
#halfway concentric circles
axes.add_patch(Ellipse((50, 50), 0.5*55/IcHx*100, 0.5*55/IcHy*100,
ec='w', fc='none',zorder=1))
axes.add_patch(Ellipse((50, 50), 1*55/IcHx*100, 1*55/IcHy*100,
ec='w', fc='none',zorder=1))
axes.add_patch(Ellipse((50, 50), 2*55/IcHx*100, 2*55/IcHy*100,
ec='w', fc='none',zorder=1))
# half-way line in UL - visual field limit on shoulders
axes.add_line(plt.Line2D([50, 50],[0, 100],c=llm_col,lw=0.5)) #50,50. 0,100
#print(xs,ys)
if ball_ref == True:
axes.add_line(plt.Line2D([xb,100],[yb,100],c='white',lw=1.0,zorder= 3))
axes.add_line(plt.Line2D([xb,0],[yb,100],c='white',lw=1.0,zorder=3))
axes.add_line(plt.Line2D([xb,0],[yb,0],c='white',lw=1.0,zorder= 3))
axes.add_line(plt.Line2D([xb,100],[yb,0],c='white',lw=1.0,zorder=3))
else:
axes.add_line(plt.Line2D([xs,100],[ys,100],c='white',lw=1.0,zorder= 3))
axes.add_line(plt.Line2D([xs,0],[ys,100],c='white',lw=1.0,zorder=3))
axes.add_line(plt.Line2D([xs,0],[ys,0],c='white',lw=1.0,zorder= 3))
axes.add_line(plt.Line2D([xs,100],[ys,0],c='white',lw=1.0,zorder=3))
if dbs==True:
#draw_blind_zone
axes.add_line(plt.Line2D([xs,75],[ys,100],c='blue',lw=2.0,linestyle='dotted',zorder=3))
axes.add_line(plt.Line2D([75,xs],[0,ys],c='blue',lw=2.0,linestyle='dotted',zorder=3))
#draw Opponent Goal reference
axes.add_line(plt.Line2D([xs,0],[ys,((100-GOAL)/2)],c='red',lw=2.0,linestyle='dotted',zorder=3))
axes.add_line(plt.Line2D([xs,0],[ys,((100-GOAL)/2)+6],c='red',lw=2.0,linestyle='dotted',zorder=3))
#draw Ball reference
axes.add_line(plt.Line2D([xs,xb-3],[ys,yb+3],c='red',lw=2.0,linestyle='dotted',zorder=3))
axes.add_line(plt.Line2D([xs,xb+3],[ys,yb-3],c='red',lw=2.0,linestyle='dotted',zorder=3))
# cognitive knowledge acquired
plt.text(45,105,'lateral',fontsize=16, color='gold') #-5,110
plt.text(45, -8,'lateral',fontsize=16, color='gold') #-5,110
plt.text(-10,40,'contralateral',fontsize=16, color='gold',rotation='vertical') #-5,110
plt.text(105,40,'contralateral',fontsize=16, color='gold',rotation='vertical') #-5,110
plt.text(40,43,'the near by',fontsize=16, color='gold') #-5,110
plt.text(40, 7,'the far away',fontsize=16, color='gold') #-5,110
plt.text(40,66,'inner',fontsize=16, color='gold') #-5,110
plt.text(40,90,'outter',fontsize=16, color='gold') #-5,110
# draw the ball
plt.scatter(xb,yb,edgecolor='black',linewidth=lw,facecolor='black',alpha=0.8,zorder=zorder,s=30)
return axes
#collapse_hide
ball_ref = False
draw_landscape_s3(ball_ref,dbs=True) # False synergon reference, True ball reference
#if ball_ref==True:
# plt.savefig('../../APimages/03landscapeUb.png') #ball_ref=True
#else:
# plt.savefig('../../APimages/03landscapeUg.png') #ball_ref=False
The canvas for the animation is Academia Emeritense’s pitch that has a 105mx68m pitch. We will use for an unbounded landscape 105mx105m dimensions.
#collapse_hide
ball_ref = True
draw_landscape_s3(ball_ref,dbs=True) # False synergon reference, True ball reference
#if ball_ref==True:
# plt.savefig('../APimages/03landscapeUb.png') #ball_ref=True
#else:
# plt.savefig('../APimages/03landscapeUg.png') #ball_ref=False
In this third-state emerges space-time because of the possibility of a second event happening on the first thing in stasis. For first time, on the positional thing can potentially act on his own body (possibility of execute an active inference decided by Gon) a transformation or action decided by the consioussness Gon, the firstman, the monad, the player.
- The set of things is a triple: {goals,ball}
- The set of agents is a singleton: {firstman} = {Gon}
- The set of events is a tuple: {stasis, transformation} = {Ball's positional-stasis, Gon's positional-change}.
Gon creates space-time with his first intentional skill of football that intents to move himself around the unbounded landscape for possession of the ball. A transformation that will cause a relational state transition from off-ball-control to on-ball-control state. Gon has discovery that football is played mainly through looking at the ball and moving to take possession and control of the ball. Gon has discovered through this underlying idea of occupy the open space where the ball is or will be. Therefore, he has to develop a set of actions or the technics of a set of intentional skills to execute on himself and on the ball in the landscape.
Gon’s positional change is a movement that can be classified as {standing, walking, jogging, running} to qualify the velocity and acceleration of Gon’s position from point p to gain point o in open space and take control of the ball.
The last cognitive lessons that Gon acquired were that
- the main static reference of aFICS are the goals and,
- the main dynamic references of aFICS is the ball location and the direction of movement of the ball
- the existence of a phase space whose coordinates are the angles from the ball-goal-middle line of unbounded landscape1
In his perception of the events in the landscape he must have both lessons into account.
Every body understand the need of a perimeter, as constrain, for playing in a landscape. A closed landscape to play is called the bounded landscape BLandscape.
#collapse_hide
# Gon needs to play in a bounded landscape and locally explore it with
# his phobeal + perpheral vision field
# and the cosmic string of rotational symmetry around origin point **o**
origin = [0,0] # choose origin
IcR = np.sqrt(IcHx**2 + IcHy**2)
#IcR
# let us assume there are goals in the middle of contralateral horizons
GOAL = 7.32/IcHy*100
def draw_Ulandscape():
"""sets up unbounded landscape, visually framed by horizon lines
returns matplotlib fig and axes bjects.
"""
fig = plt.figure(figsize=(IcHx/15,IcHy/15)) # use 15
fig.patch.set_facecolor(uls_col) # set unbounded landscape up
axes = fig.add_subplot(1, 1, 1)
axes.set_facecolor(ls_col) # set landscape up
axes.xaxis.set_visible(False) # basis vector e1 represents x=0
axes.yaxis.set_visible(False) # basis vector e2 represents y=0
axes.set_xlim(0,150) # normalize infinite points in e1 direction
axes.set_ylim(0,150) # normalize infinite points in e2 direction
axes.set_axis_off() # do not draw spindles - no measurements
axes = draw_Ulpatches(axes)
return fig, axes
def draw_Ulpatches(axes):
plt.xlim([-5,155]) # constrain further FUL e1 direction -5, 105
plt.ylim([-5,155]) # constrain further FUL e2 direction -5, 105
axes.scatter(origin[0]+75, origin[1]+75,c='w',s=30) # origin in the center of half-way line in FUL
# cosmic rotational symmetry line determines inner|wide spaces FUL
axes.add_patch(Ellipse((75, 75), 2*20/IcHx*100, 2*20/IcHy*100,ec=llm_col,fc='none'))
axes.add_patch(Ellipse((75, 75), 2*40/IcHx*100, 2*40/IcHy*100,ec=llm_col,fc='none'))
axes.add_patch(Ellipse((75, 75), 2*55/IcHx*100, 2*55/IcHy*100,ec=llm_col,fc='none'))
# Ideal Vanished Line or Omnidirectional Horizon in rotational symmetry
axes.add_patch(Ellipse((75, 75), IcR/IcHx*100, IcR/IcHy*100,ec=vfl_col,fc='none'))
# half-way line in UL - visual field limit on shoulders
axes.add_line(plt.Line2D([75, 75], [0, 150],c=llm_col,lw=1.0)) #50,50. 0,100
# diagonal basis or visual field limit lines that intersects at origin
axes.add_line(plt.Line2D([0,150],[0,150],c=vfl_col,lw=1.0)) # 0,100. 0,100
axes.add_line(plt.Line2D([0,150],[150,0],c=vfl_col,lw=1.0)) #. 0,100 100,0
# denominations of UL subspaces
plt.text(65,155,'lateral',fontsize=14, color=sid_col) # 45,105
plt.text(65, -7,'lateral',fontsize=14, color=sid_col) # 45, -7
plt.text(-10,60,'contralateral',fontsize=14, color=sid_col,rotation='vertical') #-10,40
plt.text(155,60,'contralateral',fontsize=14, color=sid_col,rotation='vertical') #105,40
# patch goals in middle of half-e1 and half-e2 horizons
axes.add_patch(plt.Rectangle(((20), (IcR-GOAL)/2), 1, GOAL,ec=llm_col,fc='none')) #100, 100-GOAL
axes.add_patch(plt.Rectangle(((IcR-20), (IcR-GOAL)/2), -1, GOAL,ec=llm_col,fc='none')) #0,100-GOAL
return axes
#collapse_hide
draw_Ulandscape()
#plt.savefig('../../APimages/03BUlandscape.png')
Gon must understands the processes to observe and perceive in the landscape. All processes share a common structure:
- Each one is "a coordinated group of **changes in the complexity of reality**.
- Phenomena that appear and disappear in his observations.
- one occurrence follows from another,
- that leads to be perceived as an "organized family of occurrences that are systematically **linked to one another** either **casually** or **functionally**This renders processes as identifable, reproducible and classificable in an evolutionary dynamics 2
1. Fixed and aligned goals locations can be used to create a phase space with two coordinates based on the angles formed from dynamic ball location to the goals during the game.↩
2. In a game cycle the team on the pitch exhibits an evolutionary style defined by formation patterns products of many unary, diadic,, triadic and n-aray synergestic actions in the actual that concatenated and iterate one after another.↩