The Space of Spaces Affordances or All Possible aFootball Flow on aPLandscape

Charles R Paez Monzon - 2020 - aNatureTechnologies

“A Space of Spaces contains all possible football flow encoded as affordances in the aFootball Universe” - aFICS Vision

6.1. Affordances of the Space of Spaces to Build Trajectories
6.2. APIN Graph as Model of the Space of Spaces on the aPLandscape
6.3. Global Affordances of APIN Graph of All Possible Football Flow on aPLandscape
1. Table 6.7.a. Network Properties of i-length APIN Graph and The Largest Component
2. Table 6.7.b. Triadic Closure Network Property APIN and its i-length pli SubGraphs

6.1. Affordances of the Space of Spaces to Build Trajectories

We choose human perception and cognition scale to model complexity in the aFootball Universe and this determine the level of description of γ-motion of ball-actions. Ball-actions are seen as transformations on the ball location en reference to the patch zonification of the aPLandscape. Our purpose is to handle uncertainty about huge number of possible ball location sequences on the aPLandscape. Therefore, “reduce disorder” means accept to handle with coherence a universal co-existence of order and disorder. This coherent complexity is kept along multiple-scales within human behavior perception and cognition.

One first assumption about is realize that

“any arbitrary ball location is associated with 1-out-of-18 patches in the aPLandscape”
“any ball-action is described as a ball location transformation from the point (xi,yi) to a point (xj,yj). Therefore, it can be modeled as a patch-i to patch-j location transformation. Still we are dealing with a huge number of all possible location transformations.
“Any point (xi,yi) in patch-i can be modeled as been the centroid (xci,yci) of patch-i and any point (xj,yj) con be assumed to be the centroid (xcj,ycj) of patch-j”. Now, we have a finite number for all possible ball-location transformation in the aFootball Universe.

Let us study this space of spaces of all possible ball actions that can happen in the interior of aPLandscape of the aFootball Universe. This would be the finite set of ideal affordances that the aPLandscape can offer to the exploration and exploitation of the environment to play football.

6.2. APIN Graph as Model of the Space of Spaces on the aPLandscape

Now, we are ready to generate all possible football flow of a ball on the aPLandscape, without the presence of any player, any team, any head coaches. Just the affordances or possible dynamics of football flow in the openness where the ball moves the fastest and the easiest on the aPLandscape.

The possible football flow ff graph will be decomposed in an atlas of football flow subgraphs of universal length-i interactions in the range of i-length interactions determined by the diameter 5 of the PL graph.

Centrality metric is computed to assign a score to each node. Let PL = (p, r) be a graph with a set of patch nodes P and a set of edge relations R. Degree centrality is defined as the number of edges incident upon a node. Farness/Peripherality of a patch v is defined as the sum of its distances to all other patches Closeness centrality is the inverse of farness, i.e. the sum of the shortest distances between a node and all the other nodes. Closeness can be regarded as a measure of how long it will take to translate the ball from patch v to all other patches sequentially (with 1-length γ-motions). Betweenness centrality quantifies the number of times a patch acts as a bridge along the shortest path between two other patches. We can see it as a measure for quantifying the aPLandscape-control of a patch on the football flow between other patches in the aPLandscape Eigenvector centrality measures the centrality of a node as a function of the centralities of its neighbors. The measure defined in this way depends both on the number of neighbors |P(i)| and the quality of its connections pj, j ∈ P(i).

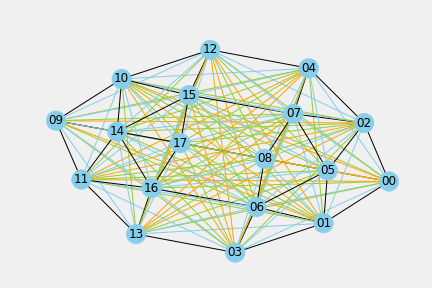
6.2.1. Affordances of 0-length ball-location interactions

Subgraph pl0 is unconnected with 18 isolated nodes.

Table 6.1.a. Network Properties of 0-length ff_pl0 Subgraph

pli	#nodes	#edges	avdegree	density	center	radius	diameter	periphery
pl0	18	18	2.0000	0.241830	infinite	infinite	infinite	infinite

Table 6.1.b All possible 0-length ball-action codes

sp	fp	0_nb_ip_fp	sp	fp	0_nb_ip_fp	sp	fp	0_nb_ip_fp
0	0	0_0_0000	1	1	0_1_0101	2	2	0_2_0202
3	3	0_3_0303	4	4	0_4_0404	5	5	0_5_0505
6	6	0_6_0606	7	7	0_7_0707	8	8	0_8_0808
9	9	0_9_0909	10	10	0_10_1010	11	11	0_11_1111
12	12	0_12_1212	13	13	0_13_1313	14	14	0_14_1414
15	15	0_15_1515	16	16	0_16_1616	17	17	0_17_1717

6.2.2. Affordances of 1-length ball-location interactions

Subgraph pl1 is connected with none isolated nodes. The central edge (8, 17), as well (3,13),(6,16),(7,15) and (4,12), is a local bridge of span 3, since the removal of this edge would increase the distance between 8 and 17 to 3. It is possible to think in the existence of obstacles whose effect would be practical as simultaneous removal of two or three central edges that increase the distance between patches in our half landscape and edges in the opponent”s half landscape edges.

Table 6.2.a. Network Properties of 1-length ff_pl1 Subgraph

pli	#nodes	#edges	avdegree	density	center	radius	diameter	periphery
pl1	18	37	4.1111	0.241830	[8,17]	3	5	[0,3,4,9,12,13]

Table 6.2.b. All possible 1-length ball-action codes

sp	fp	1_nb_ip_fp	sp	fp	1_nb_ip_fp	sp	fp	1_nb_ip_fp
0	1	‘1_3_0001’	0	2	‘1_7_0002’	0	5	‘1_17_0005’
0	5	‘1_17_0005’	1	3	‘1_11_0103’	1	5	‘1_18_0105’
1	6	‘1_23_0106’	2	4	‘1_14_0204’	2	5	‘1_19_0205’
2	7	‘1_28_0207’	3	6	‘1_24_0306’	3	13	‘1_51_0313’
4	7	‘1_29_0407’	4	12	‘1_48_0412’	5	6	‘1_25_0506’
5	7	‘1_30_0507’	5	8	‘1_33_0508’	6	8	‘1_34_0608’
6	16	‘1_65_0616’	7	8	‘1_35_0708’	7	15	‘1_60_0715’
8	17	‘1_70_0817’	9	10	‘1_40_0910’	9	11	‘1_44_0911’
9	14	‘1_54_0914’	10	12	‘1_49_1012’	10	14	‘1_55_1014’
10	15	‘1_61_1015’	11	13	‘1_52_1113’	11	14	‘1_56_1114’
11	16	‘1_66_1116’	12	15	‘1_62_1215’	13	16	‘1_67_1316’
14	15	‘1_63_1415’	14	16	‘1_68_1416’	14	17	‘1_71_1417’
15	17	‘1_72_1517’	16	17	‘1_73_1617’

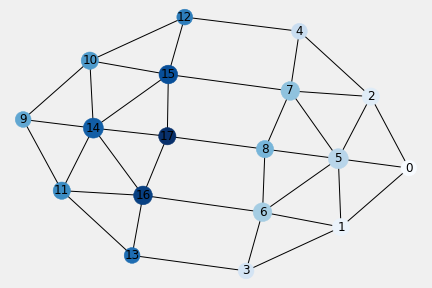
6.2.3. Affordances of 2-length ball-location interactions

Subgraph pl2 is connected with none isolated nodes.

Table 6.3.a. Network Properties of 2-length ff_pl2 Subgraph

pli	#nodes	#edges	avdegree	density	center	radius	diameter	periphery
pl2	18	52	5.7778	0.339869	all nodes	3	3	all nodes

Table 6.3.b. All possible 2-length ball-action codes

sp	fp	2_nb_ip_fp	sp	fp	2_nb_ip_fp	sp	fp	2_nb_ip_fp
0	3	2_15_0003	0	6	2_30_0006	0	4	2_20_0004
0	7	2_37_0007	0	8	2_44_0008	1	2	2_10_0102
1	13	2_72_0113	1	7	2_39_0107	1	8	2_45_0108
1	16	2_89_0116	2	12	2_67_0212	2	6	2_32_0206
2	8	2_46_0208	2	15	2_82_0215	3	5	2_25_0305
3	8	2_47_0308	3	16	2_90_0316	3	11	2_63_0311
4	5	2_26_0405	4	8	2_49_0408	4	15	2_83_0415
4	10	2_58_0410	5	16	2_91_0516	5	15	2_84_0515
5	17	2_96_0517	6	13	2_73_0613	6	7	2_40_0607
6	17	2_97_0617	6	11	2_66_0611	6	14	2_80_0614
7	12	2_68_0712	7	17	2_98_0717	7	10	2_61_0710
7	14	2_79_0714	8	16	2_92_0816	8	15	2_85_0815
8	14	2_81_0814	9	12	2_69_0912	9	15	2_86_0915
9	13	2_74_0913	9	16	2_93_0916	9	17	2_99_0917
10	11	2_62_1011	10	16	2_94_1016	10	17	2_100_1017
11	15	2_87_1115	11	17	2_101_1117	12	14	2_77_1214
12	17	2_102_1217	13	14	2_78_1314	13	17	2_103_1317
15	16	2_95_1516

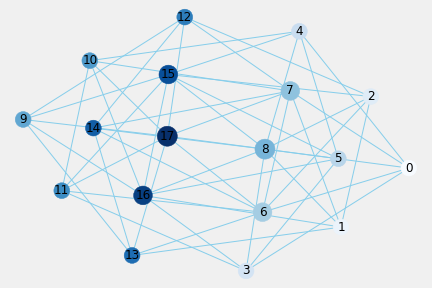
6.2.4. Affordances of 3-length ball-location interactions

Subgraph pl3 is connected with none isolated nodes.

Table 6.4.a. Network Properties of 3-length ff_pl3 Subgraph

pli	#nodes	#edges	avdegree	density	center	radius	diameter	periphery
pl3	18	43	4.7778	0.281045	all nodes	3	3	all nodes

Table 6.4.b. All possible 3-length ball-action codes

sp	fp	3_nb_ip_fp	sp	fp	3_nb_ip_fp	sp	fp	3_nb_ip_fp
0	13	3_63_0013	0	16	3_77_0016	0	12	3_58_0012
0	15	3_73_0015	0	17	3_81_0017	1	4	3_20_0104
1	11	3_54_0111	1	15	3_74_0115	1	17	3_82_0117
1	14	3_72_0114	2	3	3_15_0203	2	10	3_49_0210
2	16	3_78_0216	2	17	3_83_0217	2	14	3_70_0214
3	7	3_34_0307	3	17	3_84_0317	3	14	3_69_0314
3	9	3_45_0309	4	6	3_30_0406	4	17	3_85_0417
4	14	3_68_0414	4	9	3_43_0409	5	13	3_64_0513
5	12	3_59_0512	5	11	3_57_0511	5	14	3_71_0514
5	10	3_52_0510	6	15	3_75_0615	6	9	3_46_0609
6	10	3_50_0610	7	16	3_79_0716	7	9	3_44_0709
7	11	3_55_0711	8	13	3_65_0813	8	11	3_56_0811
8	12	3_60_0812	8	10	3_51_0810	8	9	3_47_0809
10	13	3_66_1013	11	12	3_61_1112	12	16	3_80_1216
13	15	3_76_1315

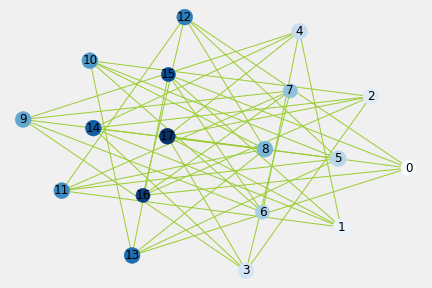
6.2.5. Affordances of 4-length ball-location interactions

Subgraph pl4 is connected with none isolated nodes.

Table 6.5.a. Network Properties of 4-length ff_pl4 Subgraph

pli	#nodes	#edges	avdegree	density	center	radius	diameter	periphery
pl4	18	18	2.0000	0.117647	[0,1,2,9,10,11] 4	6	[6,7,15,16]

Table 6.5.b. All possible 4-length ball-action codes

sp	fp	4_nb_ip_fp	sp	fp	4_nb_ip_fp	sp	fp	4_nb_ip_fp
0	11	4_25_0011	0	14	4_33_0014	0	10	4_22_0010
1	12	4_27_0112	1	9	4_20_0109	1	10	4_23_0110
2	13	4_30_0213	2	9	4_18_0209	2	11	4_26_0211
3	4	4_12_0304	3	15	4_34_0315	3	10	4_21_0310
4	16	4_35_0416	4	11	4_24_0411	5	9	4_19_0509
6	12	4_28_0612	7	13	4_31_0713	12	13	4_32_1213

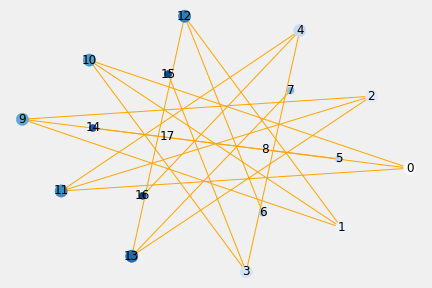
6.2.6. Affordances of 5-length ball-location interactions

Subgraph pl5 is low connected with twelve isolated nodes.

Table 6.6.a. Network Properties of 5-length ff_pl5 Subgraph

pli	#nodes	#edges	avdegree	density	center	radius	diameter	periphery
pl5	18	3	0.3333	0.019607			1

Table 6.6.b. All possible 5-length ball-action codes

sp	fp	1_nb_ip_fp	sp	fp	5_nb_ip_fp	sp	fp	5_nb_ip_fp
0	9	5_3_0009	3	12	5_4_0312	4	13	5_5_0413

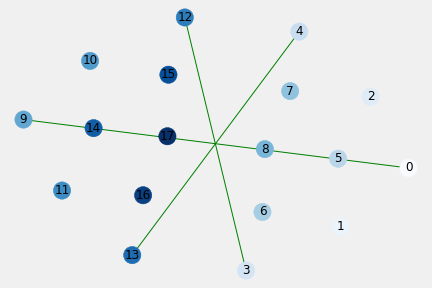
6.3. Global Affordances of APIN Graph of All Possible Football Flow on aPLandscape

Table 6.7.a. Network Properties of i-length APIN Graph and The Largest Component

pli	#nodes	#edges	avdegree	density	center	radius	diameter	periphery
APIN	18	171	19.0000	1.117647	all nodes	1	1	all nodes

The most relevant network property of the entire connected APIN graph is its uniformity. Any patch in the aPLandscape exhibits:

the same eigenvalue centrality 0.235702
the same betweenness centrality 0.0
the same closeness centrality 1.0
the same eccentricty 1 and,

Triadic closure is a measure of the tendency of edges in a graph to form triangles. It's a measure of the degree to which nodes in a graph tend to cluster together.

The APIN graph exhibits a triadic clousure of 1.0 that means each patch in the aPLandscape exhibits the tendency to cluster with any other patch and form triangles in the aPLandscape. Therefore, from any patch we can interact with any other without preferences, but when whe study in detail the set of 1, 2 and 3-length interaction these tendency are constrained by neighborhood. This is a tactical ball-actions of use 0-, 1-, 2- and, 3-length interactions while 4- and 5-length interactions are strategic ball movements for football flow.

There is a phenomenon known as the strength of weak ties, 4-length and 5-length interactions in our aPLandscape, that explain the strategic use of those interactions to superdiffuse the ball flow to the opponent goal’s patch.

Other important phenomenon for football flow fluity is the ‘triad’ concept. If two patches in the aPLandscape -PL graph- have a patch in common - 1-length neighbor-, then there is an increased likelihood that they will interact with themselves at some point in the future. This property con be measured by a local clusteriong coefficient cc.

Table 6.7.b. Triadic Closure Network Property APIN and its i-length pli SubGraphs

TC-pl0	TC-pl1	TC-pl2	TC-pl3	TC-pl4	TC-pl5	TC-APIN
0	0.387096	0.276923	0.219512	0.0	0.0	1.0